Bresenhams segmentplotalgoritme

Den Bresenham Segment Plot algoritme er en algoritme utviklet av Jack E. Bresenham iMai 1962, mens du jobbet i et IBM datalaboratorium og ønsket å kjøre en plotter festet til en tekstkonsoll. Denne algoritmen ble presentert på ACM- konvensjonen i 1963 , deretter publisert i 1965 i IBM Systems Journal .

Algoritmen bestemmer hvilke punkter i et diskret plan som skal tegnes for å danne et linjestykke tilnærming mellom to gitte punkter. Denne algoritmen brukes ofte til å tegne linjesegmenter på en dataskjerm eller et bilde beregnet for utskrift. Det regnes som en av de første algoritmene som ble oppdaget innen bildesyntese .

Bruker

Beregningsprinsippet er mye dokumentert og har siden blitt brukt til å plotte inkrementelt en konisk kurve ( sirkel , ellips , bue , parabel , hyperbola ) eller Bézier-kurver takket være egenskapene til deres definisjon av polynomfunksjon, som derivatene gjør det mulig for. å beregne orienteringene til elementære segmenter med enkle heltalloperasjoner. Man kan til og med tilpasse den til tilnærming av kurver som man bare kjenner til en begrenset utvikling av (som man kun tar de første vilkårene i svak grad), som kan brukes med god presisjon på et felt som er tilstrekkelig sammenlignet med oppløsningen ( sinusoider , eksponensial , ikke-heltall krefter ).

Algoritmen er også lett å tilpasse til beregning av kurver og overflater i et diskret rom med mer enn 2 dimensjoner (spesielt for styring av maskinverktøy). Selv i to dimensjoner kan vi med denne algoritmen diskretisere en kurve med en utjevningsfunksjon som tar hensyn til feilen som er gjort mellom to kandidatpoeng for å justere fargen, den inkrementelle feilen kan konverteres til en gjennomsiktighetskoeffisient, som holder fettet ( visuell tykkelse) av en kurve mens trappeffekten ( aliasing ) begrenses .

Denne algoritmen brukes også til utjevning av gjengivelser av 2D- teksturer som brukes på overflater av en 3D-scene der teksturen reduseres eller forstørres. Den brukes også til utjevning av fotografiske forstørrelser, eller til interpolering av mellomfarger i diskret skala.

Forklaring av den grunnleggende algoritmen i første oktant

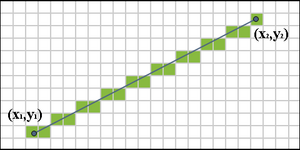
Linjen er tegnet mellom to punkter ( x 1 , y 1 ) og ( x 2 , y 2 ), hvor hvert par indikerer henholdsvis kolonnen og raden, og øker til høyre og bunn. Vi vil i utgangspunktet anta at segmentet vårt faller nedover og til høyre, og at den horisontale avstanden x 2 - x 1 overstiger den vertikale avstanden y 2 - y 1 (dvs. at segmentet har en helling mellom 0 og -1). Målet vårt er, for hver kolonne x mellom x 1 og x 2 , å identifisere raden y i den kolonnen som er nærmest det ideelle segmentet og å plotte en piksel på ( x , y ).

Bestemmelse av ordinater

Det er nå et spørsmål om å bestemme hvilken piksel som er nærmest linjen for en gitt kolonne. Den generelle formelen for en linje mellom de to punktene er gitt av:

y-y_ {1} = {\ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}} \ cdot \ left (x-x_ {1} \ høyre)

. (1)

Siden kolonnen er kjent, gis raden av pikselet nærmest den nøyaktige ordinaten til abscissapunktet på linjen ved å avrunde denne ordinaten $y$ til nærmeste heltall: $\ dot {x}$ ${\ dot {y}}$ $x = {\ dot {x}}$

{\ dot {y}} = \ left \ lfloor {\ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}} \ cdot \ left ({\ dot {x}} -x_ {1} \ høyre) + y_ {1} +0,5 \ høyre \ rgulv

. (2)

Verdien 0,5 på høyre side er en tilnærming av koordinatene (punktet er midt på firkanten).

Imidlertid er det dyrt å beregne denne verdien eksplisitt for hver kolonne . Imidlertid starter på , og hver gang vi legger til 1 til abscissen, vi legger den konstante verdi til verdien av ordinaten $y$ til punktet for den tilsvarende linje. Denne verdien er stigningen på linjen, og etter vår første antagelse er den mellom 0 og -1. Etter avrunding, for hver kolonne , bruker vi derfor enten den forrige verdien (ordinaten til abscissapikslet ), eller denne verdien økte med 1. $\ dot {x}$ $\ left ({\ dot {x}}, {\ dot {y}} \ right)$ $(x_ {1}, y_ {1}) \$ $e _ {{(1,0)}} = {\ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}}$ $\ dot {x}$ ${\ dot {y}}$ ${\ dot {x}} - 1$

Vi kan bestemme hvilke av disse to verdiene vi skal ta ved å holde en feilverdi som representerer den vertikale avstanden mellom den nåværende verdien og den eksakte $y-$ verdien for linjen ved gjeldende abscisse . I begynnelsen er denne feilverdien e null, og hver gang vi øker , øker vi feilverdien med den ovennevnte stigningsverdien. Hver gang feilen overstiger 0,5, har linjen blitt nærmere neste verdi , så vi legger 1 til mens vi samtidig trekker 1.0 fra feilen e . ${\ dot {y}}$ $x = {\ dot {x}}$ $\ dot {x}$ ${\ dot {y}}$ ${\ dot {y}}$

Fremgangsmåten ser slik ut, forutsatt at det er en grafisk primitiv tegning av piksel av rad x og kolonne $y$ ; uttrykt i pseudokode , er den grunnleggende algoritmen: tracerPixel(x, y)

procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est déclarer entier x, y, dx, dy ; déclarer rationnel e, e(1,0), e(0,1) ; // valeur d’erreur et incréments dy ← y2 - y1 ; dx ← x2 - x1 ; y ← y1 ; // rangée initiale e ← 0,0 ; // valeur d’erreur initiale e(1,0) ← dy / dx ; e(0,1) ← -1.0 ; pour x variant de x1jusqu’à x2par incrément de 1 faire tracerPixel(x, y) ; si (e ← e + e(1,0)) ≥ 0,5 alors // erreur pour le pixel suivant de même rangée y ← y + 1 ; // choisir plutôt le pixel suivant dans la rangée supérieure e ← e + e(0,1) ; // ajuste l’erreur commise dans cette nouvelle rangée fin si ; fin pour ; fin procédure ;

Forbedring av algoritmen for beregning med heltall

Problemet med denne enkle algoritmen er at datamaskinens mikroprosessorer er relativt sakte når de beregner over flytende punktum (og representasjonen som er foreslått ovenfor som rasjonelle tall for e og e (1.0) er betydelig mer kompleks og ikke naturlig støttet av prosessorer, noe som øker antallet instruksjoner for å jobbe med slike tall); dessuten akkumuleres tilnærmingsfeilene for det flytende punktet tallet e (1.0) med hvert tillegg av e (1.0) i e . Å arbeide med bare heltall vil tillate en beregning som er mer nøyaktig og raskere.

Det første trikset er å legge merke til først at vi kan erstatte e med e –0.5, som gjør det mulig å teste bare tegnet på feilverdien i stedet for å sammenligne to rasjonaliteter. Nærhetstesten med hensyn til den eksakte linjen kommer deretter ned til å vite av de to kandidatpikslene er under den nøyaktige parallelle linjen hvis ordinater økes med 0,5, og for å erstatte avrundingen med formel (1) ovenfor med nærmeste heltall ved å avrunde til et heltall lik eller mindre med denne nye linjen, som ikke endre egentlig formel (2) ovenfor, men e vil representere feilen som ble gjort under tilnærmingen av denne andre linjen med piksler som er tegnet:

procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est déclarer entier x, y, dx, dy ; déclarer rationnel e, e(1,0), e(0,1) ; // valeur d’erreur et incréments dy ← y2 - y1 ; dx ← x2 - x1 ; y ← y1 ; // rangée initiale e ← -0,5 ; // valeur d’erreur initiale e(1,0) ← dy / dx ; e(0,1) ← -1.0 ; pour x variant de x1jusqu’à x2par incrément de 1 faire tracerPixel(x, y) ; si (e ← e + e(1,0)) ≥ 0 alors // erreur pour le pixel suivant de même rangée y ← y + 1 ; // choisir plutôt le pixel suivant dans la rangée supérieure e ← e + e(0,1) ; // ajuste l’erreur commise dans cette nouvelle rangée fin si ; fin pour ; fin procédure ;

Deretter ved å multiplisere alle rasjonellene ovenfor med dx , krever ikke beregningen lenger rasjonelle trinn (som eliminerer akkumulering av tilnærmingsfeil på flottørene). Den opprinnelige verdien av e = –0,5 × dx er imidlertid ikke heltall enda, selv om trinnene er heltall.

procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est déclarer entier x, y, dx, dy ; déclarer rationnel e ; // valeur d’erreur déclarer entier e(1,0), e(0,1) ; // incréments dy ← y2 - y1 ; dx ← x2 - x1 ; y ← y1 ; // rangée initiale e ← -0,5 × dx ; // valeur d’erreur initiale e(1,0) ← dy ; e(0,1) ← -dx ; pour x variant de x1jusqu’à x2par incrément de 1 faire tracerPixel(x, y) ; si (e ← e + e(1,0)) ≥ 0 alors // erreur pour le pixel suivant de même rangée y ← y + 1 ; // choisir plutôt le pixel suivant dans la rangée supérieure e ← e + e(0,1) ; // ajuste l’erreur commise dans cette nouvelle rangée fin si ; fin pour ; fin procédure ;

Ved å doble e (og verdiene til trinnene) endrer dette imidlertid ikke noe når man tester tegnet: e vil da representere avstanden fra den eksakte ordinatlinjen økt med 0,5, denne avstanden multipliseres med faktorkonstanten positiv 2 × dy (som ikke endrer tegnet på den testede feilverdien). Hellingverdien som brukes som en økning av e blir også multiplisert med samme faktor, blir ganske enkelt 2 × dy , dens opprinnelige verdi blir - dx , den andre betingede dekning blir 2 x dx (som også kan beregnes på forhånd). Algoritmen blir da:

procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est déclarer entier x, y, dx, dy ; déclarer entier e ; // valeur d’erreur déclarer entier e(1,0), e(0,1) ; // incréments dy ← y2 - y1 ; dx ← x2 - x1 ; y ← y1 ; // rangée initiale e ← -dx ; // valeur d’erreur initiale e(1,0) ← dy × 2 ; e(0,1) ← -dx × 2; pour x variant de x1jusqu’à x2par incrément de 1 faire tracerPixel(x, y) ; si (e ← e + e(1,0)) ≥ 0 alors // erreur pour le pixel suivant de même rangée y ← y + 1 ; // choisir plutôt le pixel suivant dans la rangée supérieure e ← e + e(0,1) ; // ajuste l’erreur commise dans cette nouvelle rangée fin si ; fin pour ; fin procédure ;

Reduksjon av variabler og forenklinger

Vi kan endelig endre tegnet på e ved å teste det motsatte tegnet, og deretter redusere antall variabler ved å merke seg at x1 og y1 ovenfor ikke lenger brukes så snart den første feilen og trinnene er beregnet; det er tilstrekkelig å også endre tegnet på trinnene og nedgangene:

procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est déclarer entier dx, dy ; déclarer entier e ; // valeur d’erreur e ← x2 - x1 ; // -e(0,1) dx ← e × 2 ; // -e(0,1) dy ← (y2 - y1) × 2 ; // e(1,0) tant que x1 ≤ x2faire tracerPixel(x1, y1) ; x1 ← x1 + 1 ; // colonne du pixel suivant si (e ← e - dy) ≤ 0 alors // erreur pour le pixel suivant de même rangée y1 ← y1 + 1 ; // choisir plutôt le pixel suivant dans la rangée supérieure e ← e + dx ; // ajuste l’erreur commise dans cette nouvelle rangée fin si ; fin faire ; // Le pixel final (x2, y2) n’est pas tracé. fin procédure ;

Denne algoritmen er optimal og tilstrekkelig til å tegne en diagonal eller skrå horisontal vektor i første oktant, av økende kolonner og rader. Hvis programmeringsspråket tillater det, kan de to lokale variablene som er erklært x og y erstattes av gjenbruk av variablene x 1 og y 1 av parametrene. Denne saken er behandlet ovenfor.

Imidlertid bør det bemerkes i ovennevnte algoritme at testen av tegnet på e like godt kan inkludere likhet med null eller ikke inkludere den. Dette tilsvarer det faktum at de neste to kandidatpikslene er like langt fra den nøyaktige linjen. Hvis vi velger en diagonal forskyvning, vil det neste følgende punktet alltid oppnås ved en horisontal forskyvning; hvis man velger en horisontal forskyvning vil det neste følgende punktet alltid oppnås ved en diagonal forskyvning. Hvis vi inverterte retningen til vektoren, ville de valgte pikslene være inverterte og derfor forskjellige, og vi må ta hensyn til dette hvis vi vil ha en nøyaktig overlapping av pikslene til to skråvektorer i motsatt retning, når vi generaliserer algoritmen til skråvektorer i hvilken som helst retning (dette kan ikke skje når du tegner horisontale, vertikale eller diagonale vektorer).

Optimalisert generell algoritme

Generaliseringen av den grunnleggende algoritmen til plotting av vektorer i hvilken som helst retning oppnås ved enkel symmetri.

Algoritmen er her utviklet og optimalisert i hver av de åtte oktantene. For å sikre at de samme pikslene alltid blir tegnet for to identiske vektorer, men i motsatt retning, vil vi reversere grensefallene der en diagonal forskyvning er lik en høyre forskyvning, ved å velge diagonalen når vektoren er orientert mot venstre (avtagende abscissa) snarere enn til høyre (økende abscissa) som i det forenklede tilfellet ovenfor:

procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est déclarer entier dx, dy; si (dx ← x2 - x1) ≠ 0 alors si dx > 0 alors si (dy ← y2 - y1) ≠ 0 alors si dy > 0 alors // vecteur oblique dans le 1er cadran si dx ≥ dy alors // vecteur diagonal ou oblique proche de l’horizontale, dans le 1er octant déclarer entier e ; dx ← (e ← dx) × 2 ; dy ← dy × 2 ; // e est positif boucle sans fin // déplacements horizontaux tracePixel(x1, y1) ; interrompre boucle si (x1 ← x1 + 1) = x2 ; si (e ← e - dy) < 0 alors y1 ← y1 + 1 ; // déplacement diagonal e ← e + dx ; fin si ; fin boucle ; sinon // vecteur oblique proche de la verticale, dans le 2d octant déclarer entier e ; dy ← (e ← dy) × 2 ; dx ← dx × 2 ; // e est positif boucle sans fin // déplacements verticaux tracePixel(x1, y1) ; interrompre boucle si (y1 ← y1 + 1) = y2 ; si (e ← e - dx) < 0 alors x1 ← x1 + 1 ; // déplacement diagonal e ← e + dy ; fin si ; fin boucle ; fin si ; sinon // dy < 0 (et dx > 0) // vecteur oblique dans le 4e cadran si dx ≥ -dy alors // vecteur diagonal ou oblique proche de l’horizontale, dans le 8e octant déclarer entier e ; dx ← (e ← dx) × 2 ; dy ← dy × 2 ; // e est positif boucle sans fin // déplacements horizontaux tracePixel(x1, y1) ; interrompre boucle si (x1 ← x1 + 1) = x2 ; si (e ← e + dy) < 0 alors y1 ← y1 - 1 ; // déplacement diagonal e ← e + dx ; fin si ; fin boucle ; sinon // vecteur oblique proche de la verticale, dans le 7e octant déclarer entier e ; dy ← (e ← dy) × 2 ; dx ← dx × 2 ; // e est négatif boucle sans fin // déplacements verticaux tracePixel(x1, y1) ; interrompre boucle si (y1 ← y1 - 1) = y2 ; si (e ← e + dx) > 0 alors x1 ← x1 + 1 ; // déplacement diagonal e ← e + dy ; fin si ; fin boucle ; fin si ; fin si ; sinon // dy = 0 (et dx > 0) // vecteur horizontal vers la droite répéter tracePixel(x1, y1) ; jusqu’à ce que (x1 ← x1 + 1) = x2 ; fin si ; sinon // dx < 0 si (dy ← y2 - y1) ≠ 0 alors si dy > 0 alors // vecteur oblique dans le 2d cadran si -dx ≥ dy alors // vecteur diagonal ou oblique proche de l’horizontale, dans le 4e octant déclarer entier e ; dx ← (e ← dx) × 2 ; dy ← dy × 2 ; // e est négatif boucle sans fin // déplacements horizontaux tracePixel(x1, y1) ; interrompre boucle si (x1 ← x1 - 1) = x2 ; si (e ← e + dy) ≥ 0 alors y1 ← y1 + 1 ; // déplacement diagonal e ← e + dx ; fin si ; fin boucle ; sinon // vecteur oblique proche de la verticale, dans le 3e octant déclarer entier e ; dy ← (e ← dy) × 2 ; dx ← dx × 2 ; // e est positif boucle sans fin // déplacements verticaux tracePixel(x1, y1) ; interrompre boucle si (y1 ← y1 + 1) = y2 ; si (e ← e + dx) ≤ 0 alors x1 ← x1 - 1 ; // déplacement diagonal e ← e + dy ; fin si ; fin boucle ; fin si ; sinon // dy < 0 (et dx < 0) // vecteur oblique dans le 3e cadran si dx ≤ dy alors // vecteur diagonal ou oblique proche de l’horizontale, dans le 5e octant déclarer entier e ; dx ← (e ← dx) × 2 ; dy ← dy × 2 ; // e est négatif boucle sans fin // déplacements horizontaux tracePixel(x1, y1) ; interrompre boucle si (x1 ← x1 - 1) = x2 ; si (e ← e - dy) ≥ 0 alors y1 ← y1 - 1 ; // déplacement diagonal e ← e + dx ; fin si ; fin boucle ; sinon // vecteur oblique proche de la verticale, dans le 6e octant déclarer entier e ; dy ← (e ← dy) × 2 ; dx ← dx × 2 ; // e est négatif boucle sans fin // déplacements verticaux tracePixel(x1, y1) ; interrompre boucle si (y1 ← y1 - 1) = y2 ; si (e ← e - dx) ≥ 0 alors x1 ← x1 - 1 ; // déplacement diagonal e ← e + dy ; fin si ; fin boucle ; fin si ; fin si ; sinon // dy = 0 (et dx < 0) // vecteur horizontal vers la gauche répéter tracePixel(x1, y1) ; jusqu’à ce que (x1 ← x1 - 1) = x2 ; fin si ; fin si ; sinon // dx = 0 si (dy ← y2 - y1) ≠ 0 alors si dy > 0 alors // vecteur vertical croissant répéter tracePixel(x1, y1) ; jusqu’à ce que (y1 ← y1 + 1) = y2 ; sinon // dy < 0 (et dx = 0) // vecteur vertical décroissant répéter tracePixel(x1, y1) ; jusqu’à ce que (y1 ← y1 - 1) = y2 ; fin si ; fin si ; fin si ; // le pixel final (x2, y2) n’est pas tracé. fin procédure ;

Merknader:

Ovenfor grupperes oppgavene noen ganger i uttrykk som gjenbruker den tildelte verdien. Hvis språket som brukes ikke tillater det, er det tilstrekkelig å utføre de interne oppgavene i separate tidligere oppgaveanvisninger, og å lese denne variabelen på nytt i det inneholder uttrykket.
TracePixel ( x 1 , y 1 ) grafiske primitiver er gruppert sammen over for å tegne horisontale (tilfelle av første oktant over) eller vertikale (andre oktant) segmenter i den indre sløyfen, og kan grupperes i et enkelt anrop (det er tilstrekkelig til telle antall passasjer i den interne sløyfen, og tegne det horisontale (eller vertikale) segmentet som sporer ved utgangen av denne sløyfen.

Referanser

James D. Foley, Introduksjon til datagrafikk , Paris, Addison-Wesley Frankrike,Mai 1995, 573 s. ( ISBN 978-2-87908-058-1 , varsel BNF n o FRBNF37480856 ) , s.76 til 84

(no) Jack E. Bresenham , “ Algoritme for datamaskinkontroll av en digital plotter ” , IBM Systems Journal , vol. 4, n o 1,1 st januar 1965, s. 25–30 ( DOI 10.1147 / sj.41.0025 , les online )

Relaterte artikler

Bresenhams sirkelbue-algoritme
Andres sirkelplottalgoritme
Xiaolin Wus segmentplotalgoritme , versjon med anti-aliasing