Projektilbane

I fysikk er banen til et prosjektil veien som dette prosjektilet vil ta etter å ha blitt lansert.

Med prosjektil menes et lite objekt med lav masse (for eksempel en rullestein eller en kanonkule) sammenlignet med størrelsen og massen til kroppen den drives fra (det kan være jorden, månen osv.) Med en hastighet og i en vinkel slik at den ikke kan forbli i bane og faller tilbake. I tillegg er det nødvendig at hastigheten er tilstrekkelig lav sammenlignet med lysets hastighet - at Lorentz-faktoren som karakteriserer den er tilstrekkelig nær 1 - for ikke å måtte forlate klassiske fysikkhensyn .

Når vi studerer banen til et prosjektil mens vi forsømmer alle kreftene unntatt vekten , snakker vi om en ballistisk bane . Det er enkelt å løse ligningene til den ballistiske banen til et prosjektil, men denne modelleringen er langt fra virkeligheten når andre krefter blir vurdert, for eksempel kreftene indusert av væsken som prosjektilet utvikler seg i (friksjonskrefter, skyvekraft Archimedes , etc.).

Notasjoner

I ligningene i artikkelen vil følgende variabler bli brukt:

g : den tyngdens akselerasjon i m / s 2 (9,81 m / s 2 ved overflaten av jorden );
θ eller α: rekkevidden, det vil si vinkelen som prosjektilet lanseres med, i grader ;
v 0 eller v i : starthastigheten som prosjektilet lanseres med, i m / s;
y 0 eller h : den opprinnelige høyden på prosjektilet, i meter;
d : den horisontale avstanden som prosjektilet har reist, fra startpunktet til fallpunktet på bakken, i meter.
k : proporsjonalitetskoeffisienten som er karakteristisk for væskens trekk .

For å uttrykke avstandene kan vi også bruke et ortonormalt kartesisk koordinatsystem der O er det punktet prosjektilet blir lansert fra. Vi vil kalle det koordinataksesystem som er den horisontale , det koordinataksesystem som er den vertikale , og det koordinataksesystem som er den dybde . ${\ displaystyle {\ mathcal {R}} = (O; {\ vec {i}}, {\ vec {j}}, {\ vec {k}})}$ $(Okse) = (O; {\ vec {i}})$ $(Oy) = (O; {\ vec {j}})$ $(Oz) = (O; {\ vec {k}})$

Ballistisk bane

Den ballistiske banen til et prosjektil er veien som tas av et prosjektil som er utsatt for den eneste tyngdekraften, og forsømmer alle andre krefter.

Time- og kartesiske ligninger

Teorem (ballistisk bane) - I , om vi ikke akter alle krefter, bortsett fra vekten, et prosjektil lansert ved t = 0 sekunder fra en høyde h (i meter) med en hastighet $v$ $0$ (i m / s) ved å lage en vinkel α (i radianer) mellom horisontal og vertikal, og en vinkel β (i radianer) mellom dybde og horisontal, har for koordinater (i meter) over tid (i sekunder): ${\ mathcal R}$

{\ displaystyle x \ left (t \ right) = \ cos \ left (\ alpha \ right) v_ {0} t}

{\ displaystyle y \ left (t \ right) = - {\ frac {1} {2}} gt ^ {2} + \ sin \ left (\ alpha \ right) v_ {0} t + h}

{\ displaystyle z \ left (t \ right) = \ cos \ left (\ beta \ right) v_ {0} t}

Kartesisk ligning av prosjektilet (ballistiske bane) - I , om vi ikke akter alle krefter, bortsett fra vekten, et prosjektil skytes ut fra en høyde h (i meter) med en hastighet $v$ $0$ (i m / s) i som danner en vinkel α ( i radianer) mellom det horisontale og vertikale, og en vinkel β (i radianer) mellom dybden og det horisontale, dens høyde (i meter) og dybden (i meter) som en funksjon av avstanden den har kjørt (i meter) er: ${\ mathcal R}$

{\ displaystyle y \ left (x \ right) = - {\ frac {1} {2}} {\ frac {gx ^ {2}} {\ cos ^ {2} \ left (\ alpha \ right) v_ { 0} ^ {2}}} + \ tan \ left (\ alpha \ right) x + h}

{\ displaystyle z \ left (x \ right) = x {\ frac {\ cos \ left (\ beta \ right)} {\ cos \ left (\ alpha \ right)}}}

. Demonstrasjon

Vi betrakter et prosjektil som er lansert på overflaten av et legeme hvis tyngdekraftsfelt betraktes som ensartet og vi er i en galilensk referanseramme . Dermed gjelder Newtons andre lov for vårt system, og denne forteller oss at summen av de ytre kreftene som gjelder prosjektilet er lik derivatet av dens momentum. Så det har vi gjort

{\ displaystyle \ sum _ {i} {\ vec {F}} _ {i} = {\ frac {\ mathrm {d} {\ vec {p}}} {\ mathrm {d} t}} = {\ frac {\ mathrm {d} \ left (m {\ vec {v}} \ right)} {\ mathrm {d} t}}}

hvor påføres en kraft på prosjektilet og fremdriften til prosjektilet. ${\ displaystyle {\ vec {F}} _ {i}}$ $\ vec {p} = m \ vec {vb}$

Prosjektilet endrer ikke masse under kastet, så vi kan skrive det

{\ displaystyle \ sum _ {i} {\ vec {F}} _ {i} = m {\ frac {\ mathrm {d} {\ vec {v}}} {\ mathrm {d} t}}}

Imidlertid, per definisjon, er det avledede av hastigheten med hensyn til tid akselerasjonen, derfor la ${\ displaystyle {\ frac {\ mathrm {d} {\ vec {v}}} {\ mathrm {d} t}} = {\ vec {a}}}$

{\ displaystyle \ sum _ {i} {\ vec {F}} _ {i} = m {\ vec {a}}}

På den annen side er alle kreftene ubetydelige sammenlignet med vekten . Så det har vi gjort ${\ vec {P}} = m {\ vec {g}}$

{\ displaystyle \ sum _ {i} {\ vec {F}} _ {i} = {\ vec {P}} = m {\ vec {g}} = m {\ vec {a}}}

fra hvor

{\ displaystyle {\ vec {a}} = {\ vec {g}} = {\ begin {pmatrix} 0 \\ - g \\ 0 \ end {pmatrix}}}

Vi har derfor akselerasjonsvektoren til prosjektilet. For å bestemme hastighetsvektoren er det tilstrekkelig å finne antiderivasjonen til akselerasjonsvektoren med hensyn til tid, nemlig

{\ displaystyle {\ vec {v}} = {\ begin {pmatrix} {C_ {x}} _ {v} \\ - gt + {C_ {y}} _ {v} \\ {C_ {z}} _ {v} \ end {pmatrix}}}

hvor , og er konstanter.

{\ displaystyle {C_ {x}} _ {v}}

{\ displaystyle {C_ {y}} _ {v}}

{\ displaystyle {C_ {z}} _ {v}}

Nå ved t = 0 har vi . ${\ displaystyle {\ vec {v}} = {\ begynn {pmatrix} {C_ {x}} _ {v} \\ - g \ times 0+ {C_ {y}} _ {v} \\ {C_ { z}} _ {v} \ end {pmatrix}} = {\ begynn {pmatrix} {C_ {x}} _ {v} \\ {C_ {y}} _ {v} \\ {C_ {z}} _ {v} \ end {pmatrix}} = {\ vec {v_ {0}}}}$

Og vi kjenner verdiene til komponentene i . Faktisk ved trigonometri vet vi at: ${\ vec {v_ {0}}}$

{\ displaystyle \ cos \ left (\ alpha \ right) = {\ frac {v_ {0_ {x}}} {v_ {0}}}}

{\ displaystyle \ sin \ left (\ alpha \ right) = {\ frac {v_ {0_ {y}}} {v_ {0}}}}

{\ displaystyle \ cos \ left (\ beta \ right) = {\ frac {v_ {0_ {z}}} {v_ {0}}}}

Så og så ${\ displaystyle {\ vec {v_ {0}}} = {\ begynn {pmatrix} {C_ {x}} _ {v} \\ {C_ {y}} _ {v} \\ {C_ {z}} _ {v} \ end {pmatrix}} = {\ begin {pmatrix} \ cos \ left (\ alpha \ right) v_ {0} \\\ sin \ left (\ alpha \ right) v_ {0} \\\ cos \ left (\ beta \ right) v_ {0} \ end {pmatrix}}}$

{\ displaystyle {\ vec {v}} = {\ begin {pmatrix} \ cos \ left (\ alpha \ right) v_ {0} \\ - gt + \ sin \ left (\ alpha \ right) v_ {0} \ \\ cos \ left (\ beta \ right) v_ {0} \ end {pmatrix}}}

Vi har derfor etablert hastighetsvektoren til prosjektilet som en funksjon av tiden. Imidlertid er definisjonen avledet av posisjonen som en funksjon av tid hastigheten. Ved å ta i betraktning at prosjektilet opptar punktet P av , defineres således timekoordinatene til prosjektilet ved å bestemme vektoren hvis komponenter er primitivene til komponentene i vektoren . ${\ mathcal R}$ ${\ displaystyle {\ overrightarrow {OP}}}$ ${\ vec {vb}}$

Vi har da

{\ displaystyle {\ overrightarrow {OP}} = {\ begin {pmatrix} \ cos \ left (\ alpha \ right) v_ {0} t + C_ {x_ {OP}} \\ - {\ frac {1} { 2}} gt ^ {2} + \ sin \ left (\ alpha \ right) v_ {0} t + C_ {y_ {OP}} \\\ cos \ left (\ beta \ right) v_ {0} t + C_ {z_ {OP}} \ end {pmatrix}}}

hvor , og er konstanter.

{\ displaystyle C_ {x_ {OP}}}

{\ displaystyle C_ {y_ {OP}}}

{\ displaystyle C_ {z_ {OP}}}

Nå ved t = 0 har vi og vi vet posisjonen til prosjektilet. Faktisk, starter den ved x = z = 0 fra en høyde h , derfor , og . ${\ displaystyle {\ overrightarrow {OP}} = {\ begin {pmatrix} C_ {x_ {OP}} \\ C_ {y_ {OP}} \\ C_ {z_ {OP}} \ end {pmatrix}}}$ ${\ displaystyle C_ {x_ {OP}} = 0}$ ${\ displaystyle C_ {z_ {OP}} = 0}$ ${\ displaystyle C_ {y_ {OP}} = h}$

Fra hvor

{\ displaystyle x \ left (t \ right) = \ cos \ left (\ alpha \ right) v_ {0} t}

{\ displaystyle y \ left (t \ right) = - {\ frac {1} {2}} gt ^ {2} + \ sin \ left (\ alpha \ right) v_ {0} t + h}

{\ displaystyle z \ left (t \ right) = \ cos \ left (\ beta \ right) v_ {0} t}

Vi kan nå bestemme den kartesiske ligningen til prosjektilet, det vil si høyden i henhold til avstanden den har gått.

Vi vet det

{\ displaystyle x = \ cos \ left (\ alpha \ right) v_ {0} t}

Derfor, ved å isolere t , har vi

{\ displaystyle t = {\ frac {x} {\ cos \ left (\ alpha \ right) v_ {0}}}}

Derfor, ved å erstatte dette uttrykket av t i uttrykket for komponenten y og z i timeligningen, får vi den kartesiske ligningen til prosjektilet:

{\ displaystyle y \ left (x \ right) = - {\ frac {1} {2}} {\ frac {gx ^ {2}} {\ cos ^ {2} \ left (\ alpha \ right) v_ { 0} ^ {2}}} + \ tan \ left (\ alpha \ right) x + h}

{\ displaystyle z \ left (x \ right) = x {\ frac {\ cos \ left (\ beta \ right)} {\ cos \ left (\ alpha \ right)}}}

Avstand tilbakelagt

Den totale horisontale avstanden d tilbakelagt til prosjektilet lander på bakken er gitt av:

{\ displaystyle d = {\ frac {v} {g}} \ cos \ alpha \ left (v \ sin \ alpha + {\ sqrt {(v \ sin \ alpha) ^ {2} + 2gh}} \ right) .}

Når starthøyden er lik null, beregnes avstanden som følger:

{\ displaystyle d = {\ frac {v ^ {2}} {g}} \ sin \ left (2 \ alpha \ right).}

Demonstrasjon

Her prøver vi å løse ligningen . ${\ displaystyle y \ left (x \ right) = 0}$

Nå vet vi det

{\ displaystyle y \ left (x \ right) = - {\ frac {1} {2}} {\ frac {g} {\ cos ^ {2} \ left (\ alpha \ right) v_ {0} ^ { 2}}} x ^ {2} + \ tan \ left (\ alpha \ right) x + h}

Vi kan derfor løse ligningen. Merk at uttrykket for er en kvadratisk funksjon . Vi kan derfor bruke en kvadratisk ligningsløsning. ${\ displaystyle y \ left (x \ right)}$

Så diskriminerende er: ${\ displaystyle y \ left (x \ right)}$

\ Delta = b ^ {2} -4ac

{\ displaystyle \ Delta = \ tan ^ {2} \ left (\ alpha \ right) -4 \ left (- {\ frac {1} {2}} {\ frac {g} {\ cos ^ {2} \ venstre (\ alpha \ right) v_ {0} ^ {2}}} \ høyre) h}

{\ displaystyle \ Delta = \ tan ^ {2} \ left (\ alpha \ right) + {\ frac {2gh} {\ cos ^ {2} \ left (\ alpha \ right) v_ {0} ^ {2} }}> 0}

Så har to løsninger: ${\ displaystyle y \ left (x \ right) = 0}$

{\ displaystyle d_ {1} = {\ frac {-b - {\ sqrt {\ Delta}}} {2a}}}

{\ displaystyle d_ {2} = {\ frac {-b + {\ sqrt {\ Delta}}} {2a}}}

Vi vil bare beholde løsningen d 1 , som er positiv (fordi a er negativ).

Flytid

Flytiden t er tiden det tar for prosjektilet å falle til bakken.

{\ displaystyle t = {\ frac {d} {v \ cos \ theta}} = {\ frac {v \ sin \ theta + {\ sqrt {(v \ sin \ theta) ^ {2} + 2gy_ {0} }}} {g}}.}

Maksimal høyde

Maksimal høyde h oppnådd av prosjektilet under flyturen beregnes som følger:

{\ displaystyle h = {\ frac {v_ {0} ^ {2} \ sin ^ {2} \ left (\ theta \ right)} {2g}}}

Rekkevinkel for å nå en avstand d

Rekkevinkelen er vinkelen θ som et prosjektil må lanseres for å kjøre en avstand d , med tanke på utgangshastigheten v .

{\ displaystyle \ sin (2 \ theta) = {\ frac {gd} {v ^ {2}}}}

{\ displaystyle \ theta = {\ frac {1} {2}} \ arcsin \ left ({\ frac {gd} {v ^ {2}}} \ right).}

Hastighet på avstand x

Den absolutte verdien | v | av prosjektilets hastighet i en avstand x er gitt av:

{\ displaystyle | v | = {\ sqrt {v ^ {2} -2gx \ tan \ theta + \ left ({\ frac {gx} {v \ cos \ theta}} \ right) ^ {2}}}. }

Vinkel θ nødvendig for å nå koordinatene ( x ; y )

For å oppnå et mål på avstand x og en høyde y når prosjektilet skytes fra punktet for koordinatene (0; 0) med en hastighet v , vil verdiene på området vinkel θ er beregnet som følger:

{\ displaystyle \ theta = \ arctan {\ left ({\ frac {v ^ {2} \ pm {\ sqrt {v ^ {4} -g (gx ^ {2} + 2yv ^ {2})}}} {gx}} \ høyre)}.}

Bane for et prosjektil som beveger seg i en væske

Når et prosjektil beveger seg i en væske, opplever den en dragkraft som motsetter seg bevegelsen. Denne motstandskraften er karakteristisk for prosjektilets form, hastigheten og fluidets egenskaper.

Drag er et objekt for studier av væskemekanikk , som ikke lenger vurderer bevegelsen til mobilen i væsken, men som antar den faste mobilen og deretter er interessert i strømmen av væsken rundt den. Denne strømmen er ofte kompleks, og er preget av et dimensjonsløst tall , kalt Reynolds-nummeret og bemerket : ${\ displaystyle \ mathrm {R_ {e}}}$

{\ displaystyle \ mathrm {R_ {e}} = {\ frac {v \, L \, \ rho} {\ eta}}}

med v den relative hastigheten på væsken i meter per sekund , L den karakteristiske størrelsen på strømningen i meter , ρ væskens tetthet i kilogram per kubikkmeter , og η væskens dynamiske viskositet i pascal-sekund .

Vi vet da av erfaring at:

når (det er en Stokes-strøm ), er motstanden proporsjonal med hastigheten til det bevegelige legemet: friksjonen som prosjektilet utsettes for sies å være lineær; ${\ displaystyle \ mathrm {R_ {e}} << 1}$
når (flyten er laminær ), er luftmotstanden omtrent proporsjonal med mobilens hastighet ved kraften på 1,4; ${\ displaystyle 30 <\ mathrm {R_ {e}} <800}$
når (strømmen er turbulent ), er motstanden proporsjonal med kvadratet til hastigheten til det bevegelige legemet: friksjonen som prosjektilet utsettes for, sies å være kvadratisk. ${\ displaystyle \ mathrm {R_ {e}}> 2000}$

Vi vil modellere drag som proporsjonal med hastigheten til prosjektilet hevet til en kraft λ:

{\ displaystyle F_ {T} = - k \ v ^ {\ lambda} \ quad}

med

F T

væskens trekkraft i newton , v prosjektilets hastighet, og k den karakteristiske proporsjonalitetskoeffisienten til luftmotstanden som uttrykkes i kg per sekund

tar hensyn til det arkimediske skyvet , som skyver prosjektilet i motsatt retning av tyngdefeltet, spesielt ettersom volumet er stort og væskens tetthet og intensiteten av tyngdefeltet er viktig:

{\ displaystyle {\ vec {P_ {A}}} = - \ rho \, V \, {\ vec {g}} \ quad}

med ρ væskens tetthet i kilogram per kubikkmeter og V volumet av prosjektilet i kubikkmeter.

Tilnærming ved numerisk analyse

Det antas i dette avsnittet at utviklingen av hastigheten gjøres ved en tilnærming på tangenten ved utgangspunktet ( metoden til Euler ). Fortsetter trinn for trinn, med et veldig lite trinn, er denne løsningen ekstremt tilfredsstillende, spesielt siden den er veldig enkel å implementere med en datamaskin.

Med γ presisjonsfaktoren, dvs. faktoren som definerer varigheten til en tidsenhet, så vel som med $v i$ utgangshastigheten (i m / s) til prosjektilet, dets avstandsvinkel α (i radianer) og utgangshøyden h (i meter) har vi:

{\ displaystyle x \ left (t + 1 \ right) = x \ left (t \ right) + v_ {x} \ left (t \ right) \ gamma \ quad {\ text {with}} \ quad x \ left (0 \ høyre) = 0}

{\ displaystyle y \ left (t + 1 \ right) = y \ left (t \ right) + v_ {y} \ left (t \ right) \ gamma \ quad {\ text {with}} \ quad y \ left (0 \ høyre) = h}

{\ displaystyle v_ {x} \ left (t \ right) = v_ {x} \ left (t-1 \ right) + a_ {x} \ left (t-1 \ right) \ gamma \ quad {\ text { med}} \ quad v_ {x} \ left (0 \ right) = v_ {i} \ cos \ left (\ alpha \ right)}

{\ displaystyle v_ {y} \ left (t \ right) = v_ {y} \ left (t-1 \ right) + a_ {y} \ left (t-1 \ right) \ gamma \ quad {\ text { med}} \ quad v_ {y} \ left (0 \ right) = v_ {i} \ sin \ left (\ alpha \ right)}

{\ displaystyle v \ left (t \ right) = {\ sqrt {v_ {x} \ left (t \ right) ^ {2} + v_ {y} \ left (t \ right) ^ {2}}}}

{\ displaystyle a_ {x} \ left (t \ right) = - {\ frac {1} {m}} k \ v \ left (t \ right) ^ {\ lambda -1} \ v_ {x} \ left (t \ høyre)}

{\ displaystyle a_ {y} \ left (t \ right) = - g - {\ frac {1} {m}} k \ v \ left (t \ right) ^ {\ lambda -1} \ v_ {y} \ left (t \ right) + {\ frac {1} {m}} \ rho \ V \ g}

hvor λ betegner den karakteristiske kraften til fluidmotstanden der prosjektilets hastighet er høy, og V volumet av prosjektilet fylt med fluidet.

Demonstrasjon

Vi definerer som drag som prosjektilet har gjennomgått $F_T$

{\ displaystyle F_ {T} = - k \ v ^ {\ lambda}}

Deretter skrives vektoren som representerer drag ${\ displaystyle {\ vec {F_ {T}}}}$

{\ displaystyle {\ vec {F_ {T}}} = - k \ v ^ {\ lambda -1} \ {\ vec {v}}}

Vi definerer som vektoren som representerer Archimedes-skyvekraften som utøves på prosjektilet. Så det har vi gjort ${\ displaystyle {\ vec {P_ {A}}}}$

{\ displaystyle {\ vec {P_ {A}}} = - \ rho \ V \ {\ vec {g}}}

Vi definerer som vekten av prosjektilet. Så det har vi gjort $\ vec {P}$

{\ displaystyle {\ vec {P}} = m {\ vec {g}}}

Vi plasserer oss i en galilensk referanseramme. Det antas at massen av prosjektilet forblir konstant under flyturen.

I følge Newtons andre lov kan vi derfor skrive det

{\ displaystyle \ sum _ {i} {\ vec {F}} _ {i} = m {\ vec {a}} = {\ vec {P}} + {\ vec {F_ {T}}} + { \ vec {P_ {A}}}}

{\ displaystyle {\ vec {a}} = {\ vec {g}} + {\ frac {\ vec {F_ {T}}} {m}} + {\ frac {\ vec {P_ {A}}} {m}}}

Etter Eulers metode har vi det

{\ displaystyle {\ vec {v}} \ left (t + \ Delta t \ right) \ approx {\ vec {v}} \ left (t \ right) + {\ vec {a}} \ left (t \ høyre) \ Delta t}

Deretter, med O, opprinnelsen til koordinatsystemet og P, punktet til planet okkupert av prosjektilet, på samme måte som Eulers metode gir at

{\ displaystyle {\ vec {OP}} \ left (t + \ Delta t \ right) \ approx {\ vec {OP}} \ left (t \ right) + {\ vec {v}} \ left (t \ høyre) \ Delta t}

Vi kan deretter definere sekvensene og for alle naturlige tall etter ${\ displaystyle \ left (a_ {x_ {n}} \ right)}$ ${\ displaystyle \ left (a_ {y_ {n}} \ right)}$ $ikke$

{\ displaystyle a_ {x_ {n}} = - {\ frac {1} {m}} \ k \ v ^ {\ lambda -1} \ v_ {x_ {n}}}

{\ displaystyle a_ {y_ {n}} = - g - {\ frac {1} {m}} \ k \ v ^ {\ lambda -1} \ v_ {y_ {n}} + {\ frac {1} {m}} \ \ rho \ V \ g}

og sekvensene og for alle strengt positive naturlige tall av ${\ displaystyle \ left (v_ {x_ {n}} \ right)}$ ${\ displaystyle \ left (v_ {y_ {n}} \ right)}$ $ikke$

{\ displaystyle \ left (v_ {x_ {n}} \ right): \ left \ {{\ begin {array} {ll} v_ {x_ {0}} = v_ {i} \ cos \ left (\ alpha \ høyre) \\ v_ {x_ {n}} = v_ {x_ {n-1}} + a_ {x_ {n-1}} t \ end {array}} \ right.}

{\ displaystyle \ left (v_ {y_ {n}} \ right): \ left \ {{\ begin {array} {ll} v_ {y_ {0}} = v_ {i} \ sin \ left (\ alpha \ høyre) \\ v_ {y_ {n}} = v_ {y_ {n-1}} + a_ {y_ {n-1}} t \ end {array}} \ right.}

hvor angir starthastigheten og hvor den virkelige er presisjonsfaktoren. $v_ {i}$ $t$

Til slutt definerer vi sekvensene og for alle naturlige tall etter $\ left (x_ {n} \ høyre)$ ${\ displaystyle \ left (y_ {n} \ right)}$ $ikke$

{\ displaystyle \ left (x_ {n} \ right): \ left \ {{\ begin {array} {ll} x_ {0} = 0 \\ x_ {n + 1} = x_ {n} + v_ {x_ {n}} t \ end {array}} \ right.}

{\ displaystyle \ left (y_ {n} \ right): \ left \ {{\ begin {array} {ll} y_ {0} = h \\ y_ {n + 1} = y_ {n} + v_ {y_ {n}} t \ end {array}} \ right.}

Analytisk oppløsning i kvadratisk tilfelle

Når motstanden er proporsjonal med kvadratet til prosjektilets hastighet, står man overfor et system med koblede ikke-lineære differensialligninger, og løsning krever en mer engasjert tilnærming. Newton selv klarte ikke å løse problemet, men hans samtid Johann Bernoulli lyktes etter å ha blitt utfordret av den britiske astronomen John Keill . Løsningen er kjent som hodograf-ligningen, og selv om den er den mest siterte i den fysiske litteraturen, inneholder den termer som bare kan vurderes numerisk, det vil si at denne løsningen ikke er en virkelig eksplisitt analytisk løsning.

Med ekte analytisk løsning er det nødvendig å forstå en løsning som etablerer bevegelsesligningene for alle de opprinnelige forholdene, uten å benytte tilnærminger eller forenklinger som bare er gyldige for visse spesielle tilfeller av innledende forhold. En løsning er eksplisitt hvis den eksplisitt avhenger av en naturlig uavhengig variabel, her gang, og ikke av flere andre hjelpevariabler, i likhet med hodografløsningen foreslått av Johann Bernoulli.

Så det har vi gjort

{\ displaystyle v_ {x} \ left (t \ right) = {\ frac {v_ {x_ {0}}} {\ phi \ left (t \ right)}} \ quad {\ text {with}} \ quad v_ {x_ {0}} = v_ {0} \ cos \ left (\ alpha \ right)}

{\ displaystyle v_ {y} \ left (t \ right) = {\ frac {v_ {y_ {0}} - g \ \ Phi \ left (t \ right)} {\ phi \ left (t \ right)} } \ quad {\ text {with}} \ quad v_ {y_ {0}} = v_ {0} \ sin \ left (\ alpha \ right)}

med

{\ displaystyle \ phi (t) = \ exp \ left [\ omega \ \ int _ {0} ^ {t} {\ sqrt {v_ {x} ^ {2} \ left (s \ right) + v_ {y } ^ {2} \ left (s \ right)}} \ \ mathrm {d} s \ right] \ quad {\ text {with}} \ quad \ omega = - {\ frac {k} {m}}}

{\ displaystyle \ Phi ^ {\ prime} \ left (t \ right) = \ phi \ left (t \ right)}

hvorfra det er en seriell utvikling av Maclaurin som er skrevet:

{\ displaystyle \ Phi \ left (t \ right) = \ sum _ {j = 0} ^ {+ \ infty} {\ frac {\ Phi ^ {(j)} (0)} {j!}} \ t ^ {j} \ quad}

med og , og for alle naturlige tall j ${\ displaystyle \ Phi (0) = 0}$ ${\ displaystyle \ Phi ^ {\ prime} (0) = 1}$

{\ displaystyle \ Phi ^ {(j + 2)} left (0 \ right) = \ omega \ {\ sqrt {v_ {x_ {0}} ^ {2} + \ left (v_ {y_ {0}} -g \ \ Phi ^ {(j)} \ venstre (0 \ høyre) \ høyre) ^ {2}}}}

Bestemmelse av luftmotstanden

Det erindres at med v den relative hastigheten av væsken i meter per sekund , L den karakteristiske størrelsen på strømningen i meter , ρ væskens tetthet i kilogram per kubikkmeter , og η den dynamiske viskositeten til væsken i pascal- andre . ${\ displaystyle \ mathrm {R_ {e}} = {\ frac {v \ L \ \ rho} {\ eta}}}$

Når følger strømmen en Stokes-lov . Spesielt i tilfelle en kule uttrykkes dra F T ${\ displaystyle \ mathrm {R_ {e}} << 1}$

{\ displaystyle F_ {T} = - 3 \ \ pi \ \ eta \ D \ v \ quad}

med η væskens dynamiske viskositet, D kuleens diameter og v hastigheten på det bevegelige legemet.

Deretter skrives proporsjonalitetskoeffisienten k . ${\ displaystyle k = -3 \ pi \, \ eta \, D}$

Når følger strømmen en Poiseuille-lov . ${\ displaystyle 30 <\ mathrm {R_ {e}} <800}$

Når strømmen er turbulent og motstanden F T uttrykkes ${\ displaystyle \ mathrm {R_ {e}}> 2000}$

{\ displaystyle F_ {T} = {\ frac {1} {2}} \ \ rho \ S \ C_ {x} \ v ^ {2} \ quad}

med S referanseflaten til prosjektilet, C x trekkkoeffisienten til prosjektilet.

Deretter skrives proporsjonalitetskoeffisienten . $k$ ${\ displaystyle k = {\ frac {1} {2}} \ rho \, S \, C_ {x}}$

Karakteristisk strømningsstørrelse

For studiet av drag av geometriske legemer, når objektet er profilert, er den karakteristiske størrelsen på strømmen bredden på frontflaten. Når objektet er ikke-profilert, er dette lengden på overflaten parallell med strømmen.

Volumisk masse

Den tettheten av luft er en funksjon av temperatur, molar masse og trykk. Ved å velge trykk fra den internasjonale standardatmosfæren (ISA) ved havnivå: P 0 = 101 325 Pa = 1013,25 mbar = 1013,25 hPa, kan vi vurdere at

{\ displaystyle \ rho _ {\ mathrm {air}} = 1 292 \ ganger {\ frac {273,15} {T}} \ quad}

med T i Kelvin .

Mer generelt kan man referere til tetthetstabellene for forskjellige stoffer .

Dynamisk viskositet

Sutherlands semi-empiriske lov kan brukes til å bestemme dynamisk viskositet i luft:

{\ displaystyle \ eta _ {\ mathrm {air}} = B {\ frac {\ sqrt {T}} {1 + {\ frac {c} {T}}}} \ quad}

med og empirisk bestemte konstanter, og T lufttemperaturen i kelvin .

{\ displaystyle B = 1,4810 ^ {- 6} \; \ mathrm {Ns} \ \ mathrm {K} ^ {- 0 {,} 5} \ mathrm {m} ^ {2}}

{\ displaystyle c = 119.4 \; \ mathrm {K}}

Referanseflate

Når objektet er profilert, er mobilens referanseoverflate frontflaten, det vil si overflaten okkupert av objektet på projeksjonen vinkelrett på strømmen. Når objektet ikke er profilert, er mobilens referanseflate dens flateoverflate.

Dragkoeffisient

Den motstandskoeffisient er et dimensjonsløst tall som har en verdi kan bestemmes eksperimentelt i en vindtunnel. $C_x$

Selv om dragkoeffisienten er en funksjon av Reynolds-tallet , kan vi fremdeles bruke dragkoeffisientene til bildet motsatt som en første tilnærming.

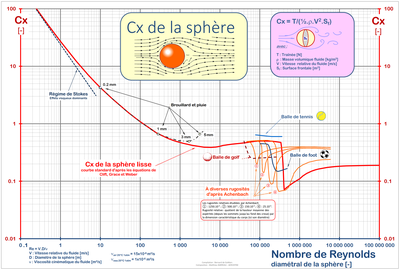
Vi kan også, i tilfelle av en sfære, henvise til denne grafen som gir trekkkoeffisienten som en funksjon av Reynolds-tallet. Innenfor visse områder av dette Reynolds-nummeret, anser ingeniører ofte sfæren som konstant. $C_x$

Merknader og referanser

Merknader

Referanser

Friksjonskrefter gjennomgått av en bevegelig gjenstand i en væske av Bernard Castaing og Hervé Gayvallet, fra École Normale Supérieure de Lyon.
"Bernoulli, J.: Responsio ad nonneminis provocationem, e until solutio quaestionis ipsi ab eodem propositae, de invenienda linea curva quam beskriver det prosjektil i medio resistente. ”I Acta Eruditorum , side 216–226 (1719)
En analytisk løsning på ligningene til bevegelsen av en punktmasse med kvadratisk motstand og generaliseringer , av Shouryya Ray og Jochen Fröhlich, publisert i Archive of Applied Mechanics i april 2015, bind 85, side 395 til 414
Air viskositet av Matthieu Schaller og Xavier Buffat (13.12.2007)